模糊聚类与WRSN

模糊关系

现实世界中,事物之间存在着这样或那样的关系.一些是界限非常明确的关系,如“父子关系”、“大小关系”等等,可以简单地用“是”与“否”或者“1”与“0”来刻画.而更多的则是界限不明显的关系,如“朋友关系”、“相近关系”、“相像关系”等.对于这类关系再用简单的“是”与“否”或者“1”与“0”来刻画显然是不合适的,必须用模糊集理论来进行描述,这就是模糊关系.
模糊关系是模糊集理论重要的内容之一,其应用范围十分广泛,几乎遍及模糊数学的所有应用领域.
本章主要介绍模糊关系的基本理论及其在聚类分析中的应用,内容主要包括：模糊矩阵,模糊关系,模糊聚类分析.

聚类算法

聚类算法是我们研究时经常遇到的算法,许多文章用其来对给定的数据集进行聚类,从而得到有利结果,以下是聚类算法的汇总.

1、层次(系统)聚类(Agglomerative Clustering)
- 1.1 凝聚层次聚类
- 1.2 分裂层次聚类
2、基于原型的聚类
3、基于密度的聚类
4、基于网格的聚类
- 4.1 STING
- 4.2 CLIQUE
5、基于图的聚类
6、基于神经网络
- 6.1 SOM

其中我们熟悉的常见聚类算法有：K-means算法、bisecting K-means等.

值得注意的是,模糊C均值聚类（FCM）算法的提出,填补了原有K-means算法的的局限性,使得聚类算法应用更加广泛.

目前许多WRSN的文章采用的聚类算法都是基于K-means的,而且都是以距离作为原始数据进行聚类,但是这样聚类的结果对于网络来说可能并不是最佳的.

模糊聚类算法

模糊聚类分析按照聚类过程的不同大致可以分为三大类：

基于模糊关系的分类法：其中包括谱系聚类算法(又称系统聚类法)、基于等价关系的聚类算法、基于相似关系的聚类算法和图论聚类算法等等.它是研究比较早的一种方法,但是由于它不能适用于大数据量的情况,所以在实际中的应用并不广泛.
基于目标函数的模糊聚类算法：该方法把聚类分析归结成一个带约束的非线性规划问题,通过优化求解获得数据集的最优模糊划分和聚类.该方法设计简单、解决问题的范围广,还可以转化为优化问题而借助经典数学的非线性规划理论求解,并易于计算机实现.因此,随着计算机的应用和发展,基于目标函数的模糊聚类算法成为新的研究热点.
基于神经网络的模糊聚类算法：它是兴起比较晚的一种算法,主要是采用竞争学习算法来指导网络的聚类过程.

模糊C均值 (FCM)

上面提到的K-均值聚类,其实它有另一个名字,C-均值聚类(HCM).要讲模糊C-均值,我们先从C-均值,也就是K-均值这个角度谈起.

HCM
从上面对K-均值算法的介绍中,我们已经知道了,K-均值的目标函数是:

$min J=\sum_{i=1}^{n}\sum_{j=1}^{c} u_{ij}d(x_{i},c_{j})$

其中,

$u_{ij}= \left{\begin{matrix} 1 & \forall k\neq j,d(x_{i},c_{j})\leqslant d(x_{i},c_{k})\ 0 & others \end{matrix}\right.$

这也是为什么叫H(Hard)CM.要么隶属该簇,要么不隶属该簇.太硬了.
引入模糊数学的观点,使得每个给定数据点用值在0,1间的隶度来确定其属于各个组的程度,便得到FCM的核心思想.
FCM

FCM的目标函数是

$J=\sum_{i=1}^{n}\sum_{j=1}^{c} u_{ij}^{m}d(x_{i},c_{j})$

其中 $u_{ij}$ 介于0,1之间;也就是说,每个样本对各个簇都有一个隶属度,不再像HCM那样要么属于,要么不属于.更”模糊”

$m\in [1,+\infty$ )为控制算法模糊程度的参数.

而且,对任意样本 $x_{i}$ 满足:

$\sum_{j=1}^{c} u_{ij}=1$

借助拉格朗日乘子,我们将限制条件整合到目标函数中得到新的目标函数

$J'=\sum_{i=1}^{n}\sum_{j=1}^{c} (u_{ij})^{m}d(x_{i},c_{j})+\sum_{i=1}^{n}\lambda_{i}(\sum_{j=1}^{c}u_{ij}-1)$

即在每一轮迭代中,要寻找 $u_{ij}$ 使得目标函数最小.

下面我们对其进行求解:
1. 当 $d_{ij}$ 为欧氏距离, $J'$ 对中心 $c_{i}$ 求偏导并令其为0,有
  
  $\frac{\partial J'}{\partial c_{j}}=\sum_{i=1}^{n}(u_{ij})^{m}x_{i}-c_{j}\sum_{j=1}^{n}(u_{ij})^{m}=0 (1)$
  
  $\Rightarrow c_{j}=\frac{\sum_{i=1}^{n}(u_{ij})^{m}x_{i}}{\sum_{i=1}^{n}(u_{ij})^{m}} (2)$
2. $J'$ 对变量 $u_{ij}$ 求偏导并令其为0,有:
  
  $\frac{\partial J'}{\partial u_{ij}}=m(u_{ij})^{m-1}\cdot d(x_{i},c_{j})+\lambda_{j} =0 (3)$
  
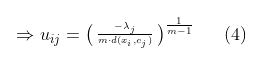
  为了使公式(4)满足条件 $\sum_{j=1}^{c} u_{ij}=1$ ,我们将公式(4)代入条件,得到:
  
  $\Rightarrow (-\lambda_{j})^{\frac{1}{m-1}} \sum_{j=1}^{c}\begin{bmatrix} \frac{1}{ m\cdot d(x_{i},c_{j}) } \end{bmatrix}^{\frac{1}{m-1}}=1$
  
  $\Rightarrow (-\lambda_{j})^{\frac{1}{m-1}}= \begin{Bmatrix} \sum_{j=1}^{c}\begin{bmatrix} \frac{1}{ m\cdot d(x_{i},c_{j}) } \end{bmatrix}^{\frac{1}{m-1}} \end{Bmatrix}^{-1} (5)$
  
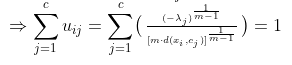
  看,我们得到了公式(5),即 $\lambda_{j}$ 所需满足的条件.接下来将公式(5)代回到公式(4),我们得到:
  
  $u_{ij}= \frac{\begin{Bmatrix} \sum_{k=1}^{c}\begin{bmatrix} \frac{1}{ m\cdot d(x_{i},c_{k}) } \end{bmatrix}^{\frac{1}{m-1}} \end{Bmatrix}^{-1}}{\begin{bmatrix} m\cdot d(x_{i},c_{j}) \end{bmatrix}^{\frac{1}{m-1}}}$
  
  $\Rightarrow u_{ij}=\frac{1}{\begin{bmatrix} m\cdot d(x_{i},c_{j}) \end{bmatrix}^{\frac{1}{m-1}} \cdot \begin{Bmatrix} \sum_{k=1}^{c}\begin{bmatrix} \frac{1}{ m\cdot d(x_{i},c_{k}) } \end{bmatrix}^{\frac{1}{m-1}} \end{Bmatrix}}$
  
  $\Rightarrow u_{ij}=\frac{1}{\sum_{k=1}^{c}\begin{bmatrix} \frac{m\cdot d(x_{i},c_{j})}{m\cdot d(x_{i},c_{k})} \end{bmatrix}^{\frac{1}{m-1}}}$
  
  $\Rightarrow u_{ij}=\frac{1}{\sum_{k=1}^{c}\begin{bmatrix} \frac{d(x_{i},c_{j})}{d(x_{i},c_{k})} \end{bmatrix}^{\frac{1}{m-1}}} (6)$
3. 数学推导到这里就结束了,我们关键再看一下公式(2)与公式(6).这两个公式分别决定了簇中心与隶属矩阵的更新.
  
  $\Rightarrow c_{j}=\frac{\sum_{i=1}^{n}(u_{ij})^{m}x_{i}}{\sum_{i=1}^{n}(u_{ij})^{m}} (2)$
  
  $\Rightarrow u_{ij}=\frac{1}{\sum_{k=1}^{c}\begin{bmatrix} \frac{d(x_{i},c_{j})}{d(x_{i},c_{k})} \end{bmatrix}^{\frac{1}{m-1}}} (6)$
模糊C均值的算法流程如下:

当算法收敛,就可以得到聚类中心和各个样本对于各簇的隶属度值,从而完成了模糊聚类划分.如果有需要,还可以将模糊聚类结果进行去模糊化.即用一定规则把模糊聚类划分为确定性分类.

聚类有效性分析

与其它基于目标函数的模糊聚类方法一样，FCM 要求在实施算法之前，必须事先指定分类数目。如果我们指定的聚类数不正确，即使使用很好的聚类算法也不会得到优的聚类结果。

然而，在实际应用中通常事先并不知道或难以确切知道样本集的聚类数。因此，根据给定样本集中数据的内在结构来自动判断样本集应该具有的聚类数(称之为佳聚类数)，是一个非常有意义的课题。这种自动寻求样本集的佳聚类数问题，我们称之为聚类有效性分析，可以借助有效性函数来实现。聚类的有效性函数，均以聚类算法的相关参数为自变量，目的是评价在选定的参数值下，算法所得的分类结果是
否或以多大程度有效地反映了数据本身固有的分类结构。经过深入研究，人们基本取得一致的认识：反映聚类有效性的主要特征是类内的紧致性和类间的分离性，因而人们设计的聚类有效性函数，都始于这一基本出发点。
已经提出的聚类有效性函数有许多，并且人们还在逐步改进。比较有代表性的有如下几个。

划分系数

如果将给定样本集分成 c 类，对应的模糊划分矩阵为 U = ( μ ij)c×n，则相应的划分系数为

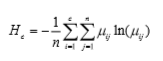
Fc的大值对应于佳的聚类数 c*。

平均模糊熵

如果将给定样本集分成 c 类，对应的模糊划分矩阵为 U = ( μ ij)c×n，则相应的平均模糊熵为

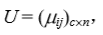
Hc的小值对应于佳的聚类数 c*。

变差−−分离度

如果将给定样本集分成 c 类，对应的模糊划分矩阵为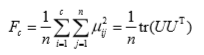聚类中心矩阵为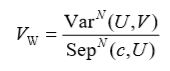
vi为第 i 类的聚类中心向量，则相应的变差−−分离度为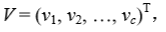

Vw的小值对应于佳的聚类数 c*，其中

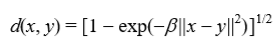
我们称 Var(U, V) 为变差度，其定义如下：

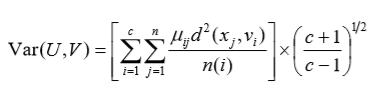
这里，n(i) 是第 i 类的样本数，d(x, y) 是一个度量，定义为：

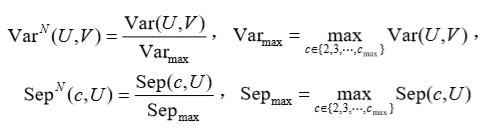
式中

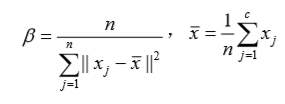
变差度所反映的是样本集整体的平均类内分散程度，分类的效果越好，类内的数据越紧密，变差度就越小。

称 Sep(c, U) 为分离度，其定义如下：

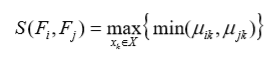
式中

分离度通过模糊集之间的不相似性来描述各个类之间的隔离程度，分类效果越好，分离度越大。
注：佳聚类数 c* 的求取，通常是对 c = 2, 3, …, cmax 逐次实施模糊聚类算法，然后根据相应的模糊划分矩阵 U 和聚类中心矩阵 V 计算有效性函数值，后比较得出佳的聚类数 c*。在实际应用中，需要处理的数据集其样本数可能非常大，但真实的分类数并不很大。因而通常取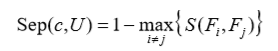，或者根据实际情况将cmax 限定的更小，以减少算法运行的费用。

FCM代码演示
```
import numpy as np
import matplotlib.pylab as plt
from sklearn.cluster import KMeans
from skfuzzy.cluster import cmeans

cp = np.random.uniform(1, 100, (100, 2))
train = cp[:50]
test = cp[50:]
train = train.T

center, u, u0, d, jm, p, fpc = cmeans(train, c=3, m=2, error=0.005, maxiter=1000)
for i in u:
    label = np.argmax(u, axis=0)

for i in range(50):
    if label[i] == 0:
        plt.scatter(train[0][i], train[1][i], c='r')
    elif label[i] == 1:
        plt.scatter(train[0][i], train[1][i], c='g')
    elif label[i] == 2:
        plt.scatter(train[0][i], train[1][i], c='b')
plt.show()
```
输出图像：

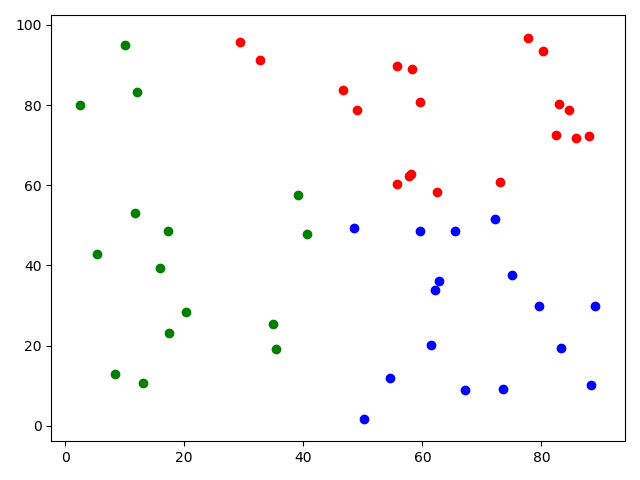
参数：
- data：训练数据，这里需要注意data的格式，应为(特征数目，数据个数)，与很多训练数据的shape正好相反。
- c：需要指定的聚类个数。
- m：隶属度指数，是一个加权指数，一般为2 。
- error：当隶属度的变化小于此则提前结束迭代。
- maxiter：最大迭代次数。
返回值：
- cntr：聚类中心
- u：最后的隶属度矩阵
- u0：初始化的隶属度矩阵
- d：是一个矩阵，记录每一个点到聚类中心的欧式距离
- jm：是目标函数的优化历史
- p：p是迭代的次数
- fpc：全称是fuzzy partition coefficient，是一个评价分类好坏的指标，它的范围是0到1, 1表示效果最好，后面可以通过它来选择聚类的个数。
参考链接

https://liangyaorong.github.io/blog/2017/%E8%81%9A%E7%B1%BB%E7%AE%97%E6%B3%95%E5%A4%A7%E7%9B%98%E7%82%B9/#1

https://blog.csdn.net/WWWQ2386466490/article/details/80349239

https://www.pythonf.cn/read/144212

http://grs.dlmu.edu.cn/__local/B/33/BD/9D3B5A6B993880F956A22B52622_B2DB6898_5B08F.pdf

模糊聚类与WRSN

模糊聚类与WRSN

模糊关系

聚类算法

模糊聚类算法

模糊C均值 (FCM)

聚类有效性分析

FCM代码演示

参考链接

感谢您的支持，我会继续努力的!